Fungsi kuadrat yang memotong sumbu x di x = α dan x = β adalah sebagai berikut
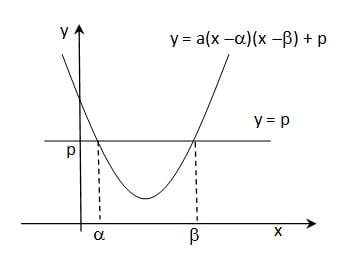
Fungsi kuadrat yang memotong y=p di x = α dan x = β adalah sebagai berikut
Fungsi kuadrat yang memotong garis y=mx + n di x = α dan x = β adalah sebagai berikut
Contoh Soal 1 :
Parabola yang memotong garis y = 6 di x = 2 dan x = 4 serta melalui (5, 3). Persamaan parabola tersebut adalah …
Jawab :
y = a(x — 2)(x — 4) + 6
Karena melalui (5, 3) kita bisa mensubtitusikan x =5 dan y = 3
3 = a(5 — 2)(5 — 4)
3 = 3a
a = 1
Jadi persamaan parabola adalah
y = 1.(x — 2)(x — 4) + 6
y = x2 — 6x + 8 + 6
y = x2 — 6x + 14
Contoh Soal 2 :
Diketahui fungsi kuadrat f(x) = ax2 + bx + c melalui titik (2, 10), (6, 10), dan (5, 4). Nilai a + b + c = …
Jawab :
Grafik melalui (2, 10) dan (6, 10), artinya grafik memotong garis y = 10 di x = 2 dan x = 6.
Dengan demikian persamaannya bisa ditulis menjadi
f(x) = a(x – 2)(x – 6) + 10
Karena melalaui (5, 4) maka f(5) = 4
a(5 – 2)(5 – 6) + 10 = 4
–3a = -6
a = 2
sehingga persamaannya menjadi
f(x) = 2(x – 2)(x – 6) + 10
f(x) = 2(x2 – 8x + 12) + 10
f(x) = 2x2 – 16x + 34
maka a + b + c = 2 – 16 + 34 = 20
Contoh soal 3
Suatu fungsi kuadrat memotong garis y = 3x + 1 di x = –1 dan x = 5. Jika fungsi melalui (4, –7) maka persamaan grafik fungsi tersebut adalah …
Jawab :
fungsi kuadrat memotong garis y = 3x + 1 di x = –1 dan x = 5 maka
y = a(x + 1)(x – 5) + 3x + 1
Karena melalui (4, –7) maka
–7 =a(5)(–1) + 12 + 1
–20 = –5a maka a = 4
Jadi
y = 4(x + 1)(x – 5) + 3x + 1
y = 4(x2 – 4x – 5) + 3x + 1
y = 4x2 – 16x – 20 + 3x + 1
y = 4x2 – 13x – 19
Contoh soal 4 :
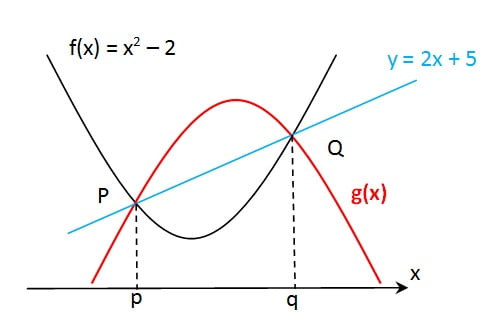
Parabola f(x) = x2 – 2 memotong garis y = 2x + 5 di P dan Q. Parabola g(x) melalui P, Q, dan (2, 30). Parabola g(x) memiliki persamaan …
Jawab :
Untuk lebih mudahnya kita buat gambar sebagai berikut :
Tampak bahwa parabola f(x) = x2 – 2 dan garis y = 2x + 5 berpotongan di x = p dan x = q, artinya p dan q bisa dicari dengan menyamakan
x2 – 2 = 2x + 5
x2 – 2x – 7 = 0
persamaan kuadrat ini jika diselesaiakan diperoleh x = p dan x = q, jadi
x2 – 2x – 7 = (x – p)(x – q) ……………………………………(1)
Karena parabola g(x) jiha melalui P dan Q maka
g(x) = a(x – p)(x – q) + 2x + 5
Dengan memakai persamaan (1) maka diperoleh
g(x) = a(x2 – 2x – 7) + 2x + 5
g(x) juga melalaui (2, 3) maka
g(2) = 30
a(4 – 4 – 7) + 4 + 5 = 30
–7a = 21 maka a = –3
Jadi
g(x) = –3(x2 – 2x – 7) + 2x + 5
g(x) = –3x2 + 6x + 21 + 2x + 5
g(x) = –3x2 + 8x + 26
Hubungan Fungsi Kuadrat Dan Garis
Koordinat Titik Puncak Fungsi Kuadrat
Kecekungan Grafik Fungi Kuadrat
Soal Soal Fungsi Kuadrat Yang Jarang Ditemukan
Titik Titik Potong Fungsi Kuadrat
Penggunaan Definit Pada Fungsi Kuadrat