Berikut ini kami sajikan soal-soal fungsi kuadrat yang jarang ditemukan. Mungkin beberapa siswa jika menemui soal ini akan kesulitan mengerjakannya. Untuk itu soal-soal kami sajikan beserta pembahasannya.
Contoh soal 1 :
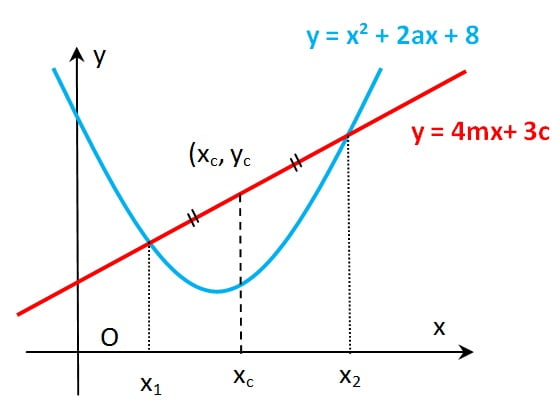
Parabola y = x2 + 2ax + 8 dan garis y = 4mx + 3c berpotongan di titik A dan B. Titik C membagi ruas garis AB menjadi dua sama panjang. Maka ordinat titik C adalah
Jawab :
Perhatikan gambar berikut
Untuk mendapatkan x1 dan x2 kita tinggal memotongkan parabola dan garis
x2 + 2ax + 8 = 4mx + 3c
x2 + (2a – 4m) x + 8 – 3c = 0
dari persamaan ini kita peroleh x1 dan x2 sehingga

Karena xc berada di tengah tengah x1 dan x2 maka

(xc, yc) terletak pada garis y = 4mx + 3c sehingga bisa disubtitusikan ke persamaan garis ini
yc = 4mxc + 3c

yc = –2ma + 4m2 + 3c
Contoh soal 2 :
Diketahui garis melalui titik O (0,0) dan memotong parabola y = x2 — 11x + 18 di titik A dan B. Jika OA = AB, maka himpunan persamaan garis OB adalah
(A) { y = 0, y = 18x}
(B) { y = 2x, y = 10x}
(C) {y = — 2x, y = – 18x}
(D) { y = 10x , y = — 20x}
(E) { y = –2x , y = –20x}
Jawab :
Pertama kita gambar dulu parabola
Titik potong dengan sumbu y adalah
x = 0 maka y = 0 — 0 + 18 = 18
Titik potong dengan sumbu x adalah
y = 0
x2 — 11x + 18 = 0
(x — 2)(x — 9) = 0
x = 2 atau x = 9
Perhatikan bahwa OA = AB
Dengan O(0, 0), A(x1, y1) dan B(x2, y2)
Berarti A di tengah-tengah O dan B
Maka titik yang di tengah-tengah bisa diperoleh dari rata-ratanya
xA = (xo + xB)/2
x1 = (0 + x2)/2
maka x2 = 2x1 ……………………………………..(1)
Sementara persamaan garis OM bisa dinyatakan dengan
y — yo = m(x — xo)
(xo, yo) merupakan titik O sehingga (xo, yo) = (0, 0)
y — 0 = m(x — 0)
y = mx …………………………………………………(2)
Garis ini kita potongkan dengan parabola y = x2 — 11x + 18
x2 — 11x + 18 = mx
x2 — (m + 11)x + 18 = 0
x1.x2 = c/a = 18
dengan mensubtitusikan persamaan (1) maka
x1.2x1 = 18
2x12 = 18
x12 = 9
x1 = ±3
Untuk x1 = 3
Maka x2 = 2x1 = 6
x1 + x2 = – b/a = m + 11
3 + 6 = m + 11
m = –2
dengan menggunakan persamaan (2) maka
y = — 2x
Untuk x1 = –3
Maka x2 = 2x1 = –6
x1 + x2 = – b/a = m + 11
–3 — 6 = m + 11
m = –20
dengan menggunakan persamaan (2) maka
y = — 20x
Jadi himpunan persamaan garis OB adalah { y = –2x , y = –20x}
Contoh Soal 3 :
Tentukan persamaan garis singgung persekutuan dari parabola y = x2 — 6x + 20 dan y = — x2 + 8x — 17
Jawab :
Garis singgung pesekutuan, artinya garis ini menyinggung parabola pertama dan kedua
Misal persamaan garisnya adalah y = mx + n
Garis ini kita subtitusi dengan parabola pertama
x2 — 6x + 20 = mx + n
x2 — (m + 6)x + 20 — n = 0
Karena bersinggungan maka
D = 0
b2 — 4ac = 0
(m + 6)2 — 4.1.(20 — n) = 0
m2 + 12m + 36 — 80 + 4n = 0
m2 + 12m + 4n — 44 = 0 ………………………..(1)
Selanjutnya persamaan garis jugakita subtitusi dengan parabola kedua
mx + n = — x2 + 8x — 17
x2 + (m — 8)x + n + 17 = 0
Karena bersinggungan maka
D = 0
b2 — 4ac = 0
(m — 8)2 — 4.1.(n + 17) = 0
m2 — 16m + 64 — 4n — 68 = 0
m2 — 16m — 4n — 4 = 0 ……………………..(2)
Sekarang persamaan (1) dan (2) kita jumlahkan
m2 + 12m + 4n — 44 = 0
m2 — 16m — 4n — 4 = 0 +
2m2 — 4m — 48 = 0
m2 — 2m — 24 = 0
(m — 6)(m + 4) = 0
m = 6 atau m = — 4
Untuk m = 6
m2 + 12m + 4n — 44 = 0
36 + 72 + 4n — 44 = 0
4n = — 64
n = — 16
Jadi persamaan garisnya y = 6x — 16
Untuk m = — 4
m2 + 12m + 4n — 44 = 0
16 — 48 + 4n — 44 = 0
4n = 76
n = 19
Jadi persamaan garisnya y = — 4x + 19
Hubungan Fungsi Kuadrat Dan Garis
Koordinat Titik Puncak Fungsi Kuadrat
Lanjutan Menyusun Fungsi Kuadrat
Kecekungan Grafik Fungi Kuadrat
Titik Titik Potong Fungsi Kuadrat
Penggunaan Definit Pada Fungsi Kuadrat