Kecekungan Grafik Fungi Kuadrat

Fungsi kuadrat memiliki f(x) = ax² + bx + c memiliki derajat kecekungan, yaitu nilai mutlak a. Oleh karena itu a≠ 0, karena jika a = 0 maka grafik tidak memiliki kecekungan.

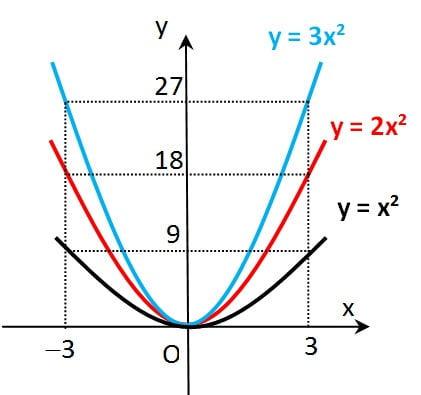
Perhatikan, apa beda grafik y = x², y = 2x², dan y = 3x². Untuk lebih mudahnya kita plot dulu dengan tabel

Jika hasil dari tabel ini digambar maka akan diperoleh gambar sebagai berikut

Nampak bahwa ketika a = 3 grafik paling cekung (warna biru). Grafik yang kecekunganny paling rendah adalah ketika a = 1 (warna hitam). Hal ini nampak jelas, bahwa nilai a menentukan kecekungan grafik.

Ketiga grafik di atas memiliki nilai a > 0, sehingga ketiganya cekung ke atas, atau sering dikatakan parabola membuka ke atas. Seandainya a < 0 maka parabola akan membuka ke bawah.

Perhatikan ketiga grafik berikut, yaitu y = –x², y = –2x², dan y = –3x².

Nampak bahwa tingkat kecekungan dari yang paling tinggi ke yang paling rendah dialami oleh a sama dengan –3, kemudian –2 dan terakhir –1. Hanya saja kecekungan di sini arahnya ke bawah. Oleh karena itu derajat kecekungan bukan ditentukan oleh a, tetapi |a|.

Untuk mengetahui lebih lanjut tentang kecekungan, sekarang kita gambar grafik

y = x² – 4x + 3

y = 2x² – 8x + 6

y = 3x² – 12x + 9

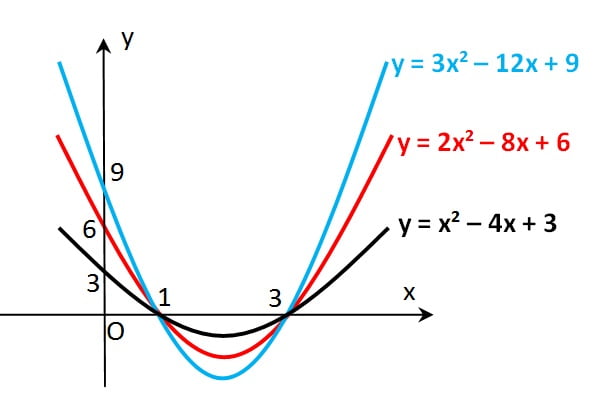
Ketiga grafik cekung ke atas dan memiliki titik potong sumbu x di titik yang sama. Perhatikan langkah berikut,

x² – 4x + 3 = 0 2x² – 8x + 6=0 3x² – 12x + 9= 0

x² – 4x + 3 = 0 2(x² – 4x + 3) = 0 3(x² – 4x + 3) = 0

(x–1)(x–3) = 0 2(x–1)(x–3) = 0 3(x–1)(x–3) = 0

x = 1 atau x = 3 x = 1 atau x = 3 x = 1 atau x = 3

Sementara titik potong sumbu y diperoleh dengan mensubtitusikan x = 0 sehingga diperoleh y = 3, y = 6, dan y = 9. Jadi, jika digambar diperoleh grafik sebagai berikut