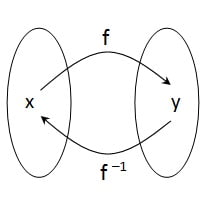
Fungsi invers berarti fungsi balikan. Artinya kita membalik domain (daerah asal) menjadi range (daerah hasil), sebaliknya range menjadi domain.
Penulisan fungsi invers f(x) adalah f-1(x).
Panah dari x ke y menyatakan
y = f(x) ………………………………………………………. (1)
sedangkan panah dari kanan ke kiri menunjukkan
x = f-1(y) ………………………………………………………(2)
Untuk lebih jelasnya kita ambil contoh-contoh berikut :
Contoh soal 1 :
Jika f(x) = 5x — 2 maka f-1 (x) = …
Jawab :
Dengan memakai persamaan (1) maka f(x) bisa kita ganti dengan y, sehingga
y = 5x — 2
maka
y + 2 = 5x
sehingga :

dengan memakai persamaan (2) maka x bisa diganti dengan f-1(y) sehingga

ini artinya

Contoh Soal 2 :
Tentukan invers dari fungsi

Jawab :
Dengan memakai persamaan (1) maka f(x) kita ganti dengan y sehingga


3y5 = 4x7 + 2
3y5 — 2 = 4x7


Dengan memakai persamaan (2) maka x kita ganti dengan f-1(y) sehingga :

Jika y diganti dengan x maka kita peroleh invers dari f(x) sebagai berikut :

Contoh soal 3 :
Invers dari fungsi

adalah …
Jawab :
Dengan memakai persamaan (1) maka f(x) bisa diganti y sehingga

2xy — 7y = 5x — 3
2xy — 5x = 7y — 3
x(2y — 5) = 7y — 3

sesuai persamaan (2) maka x bisa diganti dengan f-1(y) sehingga

sekarang y kita ganti dengan x sehingga kita peroleh invers dari f(x) sehingga :

Contoh soal 4 :
Jika f(x) = 4x3 — 12 dan diketahui f-1(a)= 2 maka nilai a sama dengan …
Jawab :
Cara I
y = 4x3 — 12
y + 12 = 4x3


maka

sehingga

Sesuai dengan soal diketahui :
f-1(a)= 2


a + 12 = 32
a = 20
cara II
dari persamaan (1) dan (2) bisa disimpulkan
Jika f-1(a) = b maka f(b) = a
Dari soal diketahui
f(x) = 4x3 — 12
karena f-1(a)= 2 maka f(2) = a sehingga :
a = f(2) = 4.23 — 12 = 32 — 12 = 20
Contoh soal 5 :
Diketahui f(x) = x3 + 2 dan  . Jika
. Jika  maka n = …
maka n = …
Jawab :
Cara I
f(x) = x3 + 2
y = x3 + 2
x3 = y — 2
sehingga :

dan

——————————-



(y — 4)3 = 2x — 7
2x — 7 = (y — 4)3
2x = (y — 4)3 + 7


—————–



————————



(n — 4)3 — 11 = 16
(n — 4)3 = 27
n — 4 = 3
n = 7
Cara II
f(x) = x3 + 2 ==> f(2) = 8 + 2 = 10
 .
.



n = g(f(2))
n = g(10)

n = 3 + 4 = 7