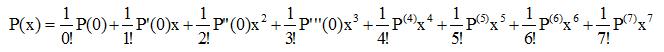Misalkan kita memiliki polinom derajat 5 sebagai berikut
P(x) = ax5 + bx4 + cx3 + dx2 + ex + f
Maka P(0) = f
Jika fungsi ini kita turunkan beberapa kali dan setiap diturunkan kita subtitusi x dengan 0 maka
P’(x) = 5ax4 + 4bx3 + 3cx2 + 2dx + e —> P'(0) = e
P’’(x) = 20ax3 + 12bx2 + 6cx + 2d —> P”(0) = 2d
P’’’(x) = 60ax2 + 24bx + 6c —> P”'(0) = 6c
P(4)(x) = 120ax + 24b —> P(4)(4) (0) = 24b
P(5)(x) = 120a —> P(5)(0) = 120a
Dengan demikian, masing-masing koefisien bisa kita tulis menjadi
f = P(0) ; e = P’(0) ; d = ½ P’’(0) ; c = ⅙ P’’’(0) ;
b = 1/24. P(4) (0) ; a = 1/120. P(5) (0)
Fungsi P(x) bisa kita tulis dengan mengubah urutannya sebagai berikut :
P(x) = f + ex + dx2 + cx3 + bx4 + ax5
dengan mengganti koefisien a, b, c, d, e, dan f maka kita peroleh
Andaikan P(x) adalah polinom derajat 6 maka kita peroleh
Seandainya P(x) adalah polinom derajat 7 maka kita peroleh
dan seterusnya.
Bentuk terakhir ini bisa juga kita tulis menjadi
Secara umum, kita bisa menuliskannya menjadi
atau
Inilah yang dimaksud dengan deret maclaurin.