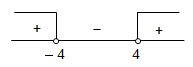Jika Persamaan Kuadrat memiliki aar-akar berlainan tanda atau berbeda tanda, artinya persmaaan kuadrat memiliki akar positif dan negatif. Nilai mutlak akarnya tidak harus sama.Jika sama (misalnya -3 dan 3 ATAU -7 dan 7) disebut akar-akar berlawanan tanda.
Jadi, akar-akar berlainan tanda di sini misalnya ( 7 dan -2), (-6 dan 1) dan sebagainya.
Agar persamaan kuadrat memiliki akar-akar berlainan tanda maka
x1 > 0 dan x2 < 0
akibatnya
x1.x2 < 0 sedangkan D > 0
Contoh soal :
Tentukan nilai p agar persamaan x2 + (p + 2)x + p +5 = 0 memiliki akar-akar berlainan tanda
Jawab :
x1.x2 < 0
p + 5 < 0
p < – 5 …………………………(1)
D > 0
b2 — 4ac > 0
(p + 2)2 — 4.1.(p + 5) > 0
p2 + 4p + 4 — 4p — 20 > 0
p2 — 16 > 0
(p — 4)(p + 4) > 0
p < -4 atau p > 4 ……………..(2)
dari (1) dan (2) diperoleh p < -5
Latihan soal
1. Agar persamaan kuadrat x2 +(m — 3)x + m + 5 = 0 memiliki akar-akar berlainan tanda maka batas-batas nilai m adalah …
2. Persamaan
Artikel terkait
akar akar rasional persamaan kuadrat
penyelesaian persamaan kuadrat
persamaan kuadrat matematika sma